球表面的小矩形到 z 轴的距离为 \( d \),投影到半径为 \( R \) 的圆柱时:
宽度拉伸比例 = \( \frac{R}{d} \)(距离 z 轴越远,拉伸比例越小)
极点附近的矩形拉伸最明显,赤道附近拉伸最弱
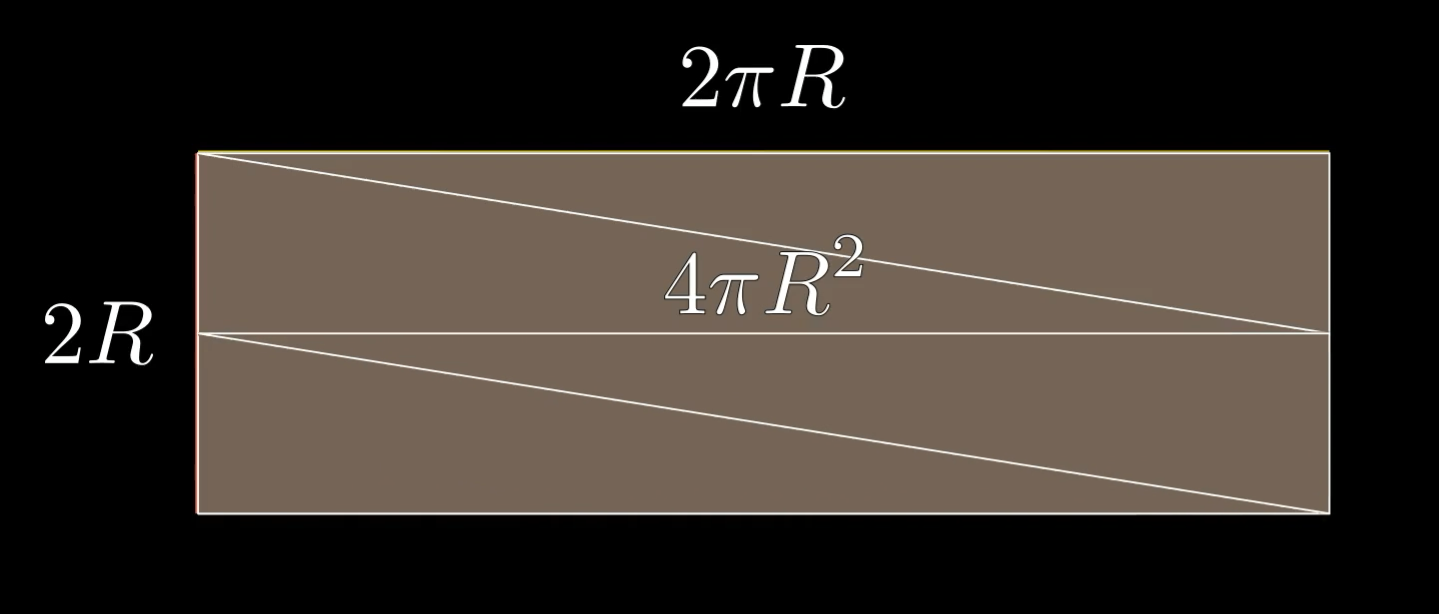
球的表面积 = 同半径、同高度的圆柱侧面积(不含上下底面)
将圆柱的侧面(不含上下底面)沿母线剪开并展开,会得到一个规则的矩形:
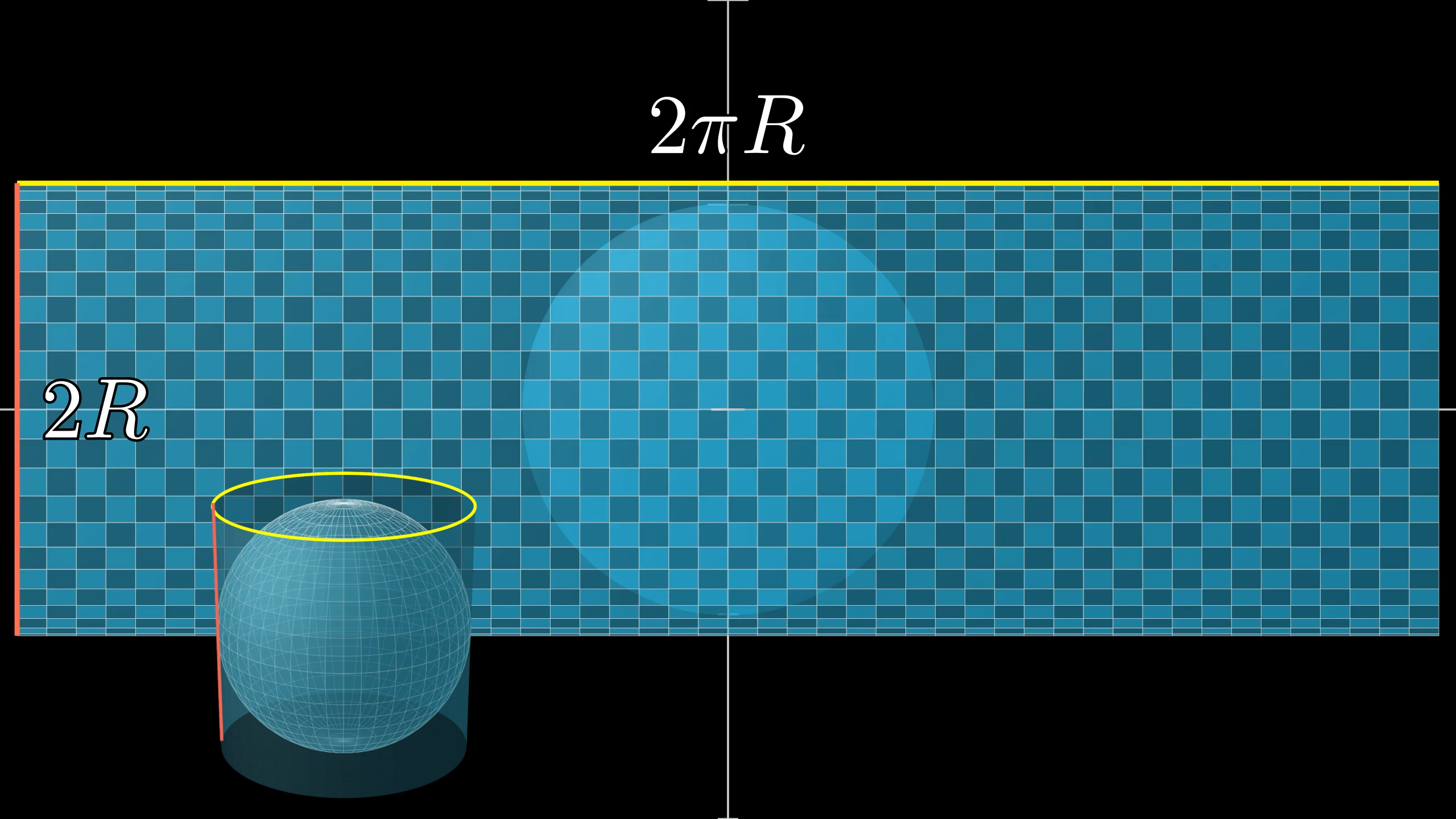
用无数个微小矩形近似覆盖球的表面,将这些小矩形沿 z 轴方向向外投影到圆柱表面:
关键:投影过程中,两个相反效应完美抵消,实现面积守恒
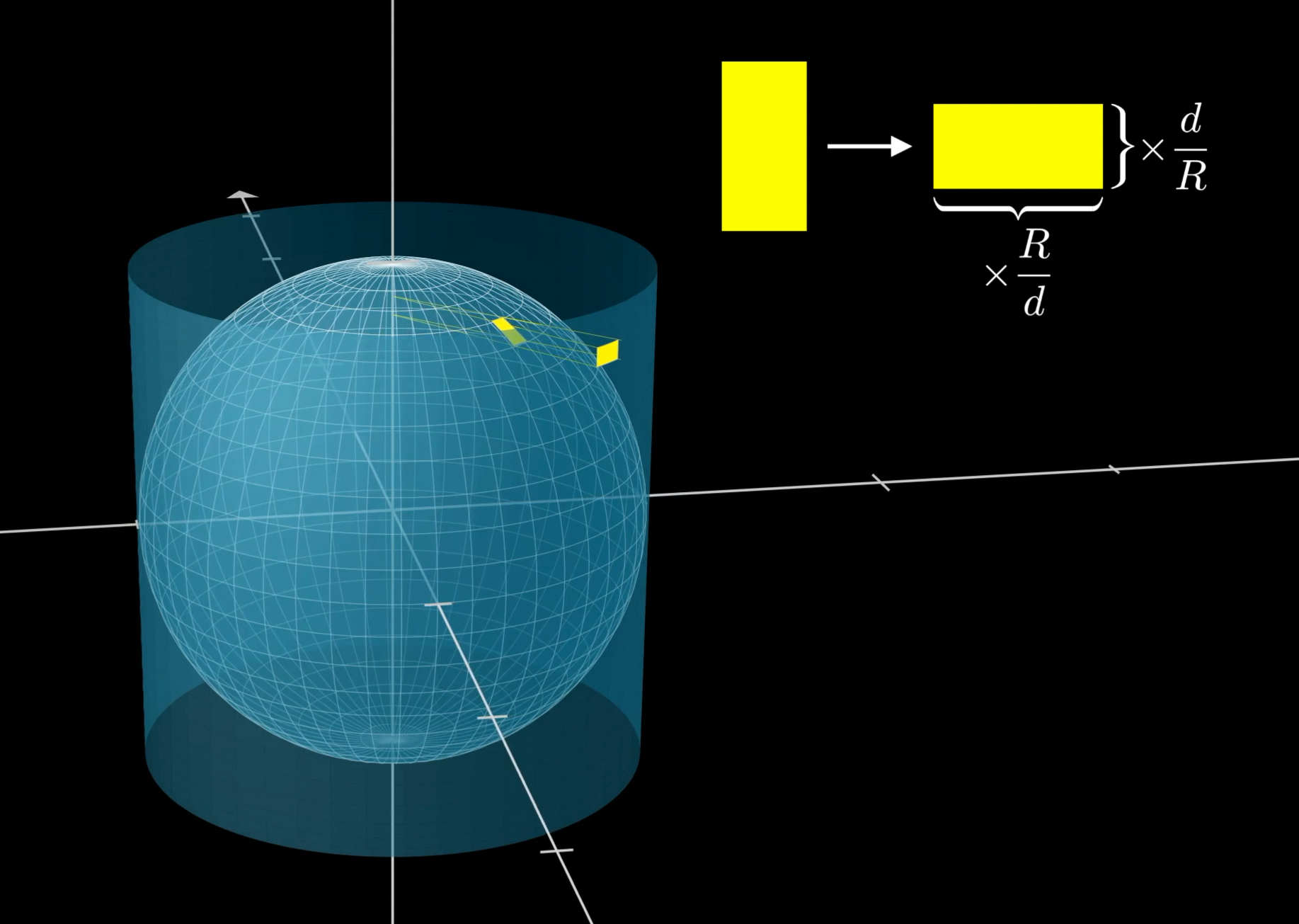
球表面的微小矩形(蓝色)投影到圆柱表面(红色),面积保持不变
球表面的小矩形到 z 轴的距离为 \( d \),投影到半径为 \( R \) 的圆柱时:
宽度拉伸比例 = \( \frac{R}{d} \)(距离 z 轴越远,拉伸比例越小)
极点附近的矩形拉伸最明显,赤道附近拉伸最弱
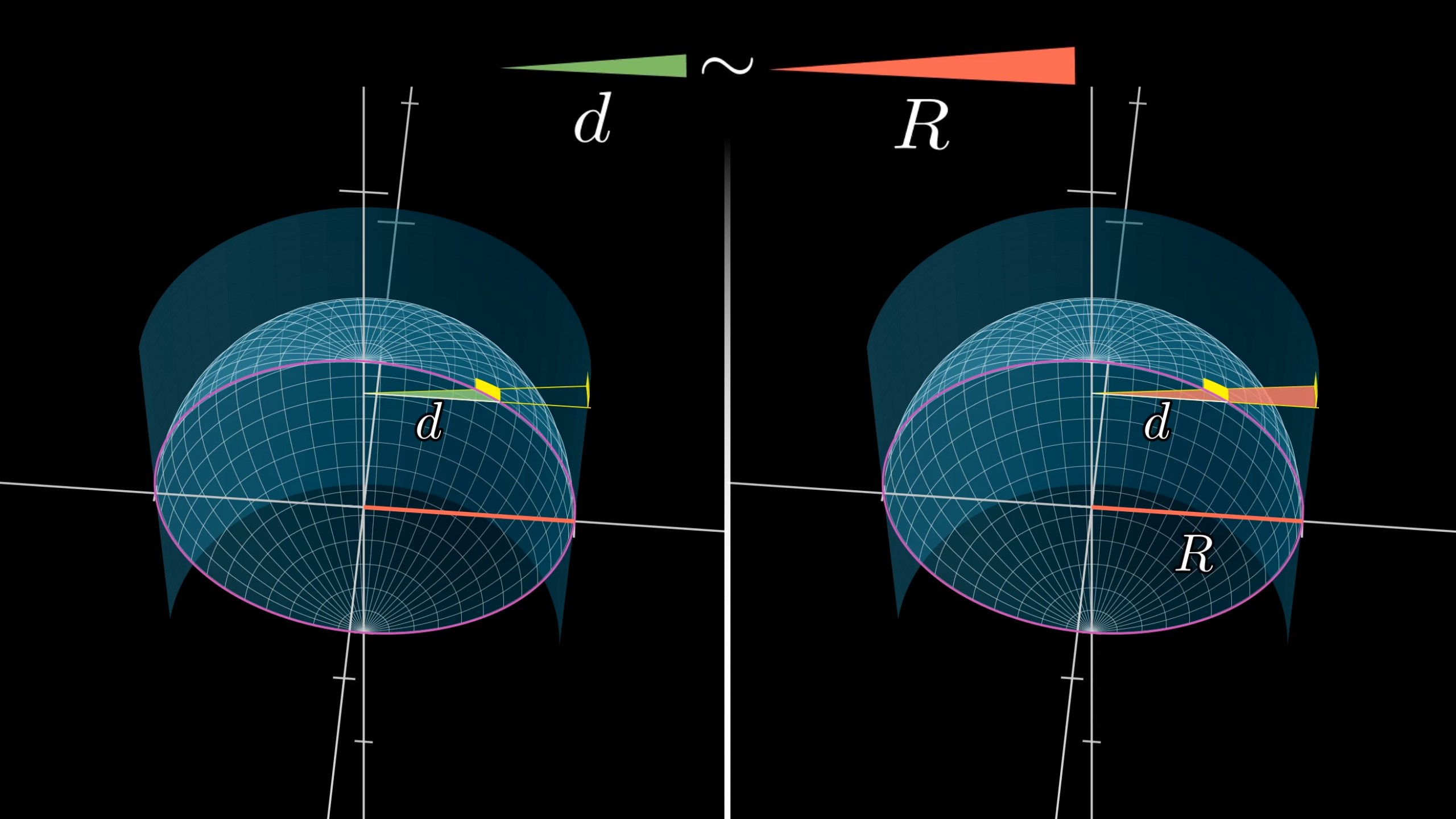
球表面的小矩形与 z 轴成倾斜角,投影时高度会被压缩:
高度压缩比例 = \( \frac{d}{R} \)(倾斜角越大,压缩比例越大)
极点附近的矩形压缩最明显,赤道附近压缩最弱
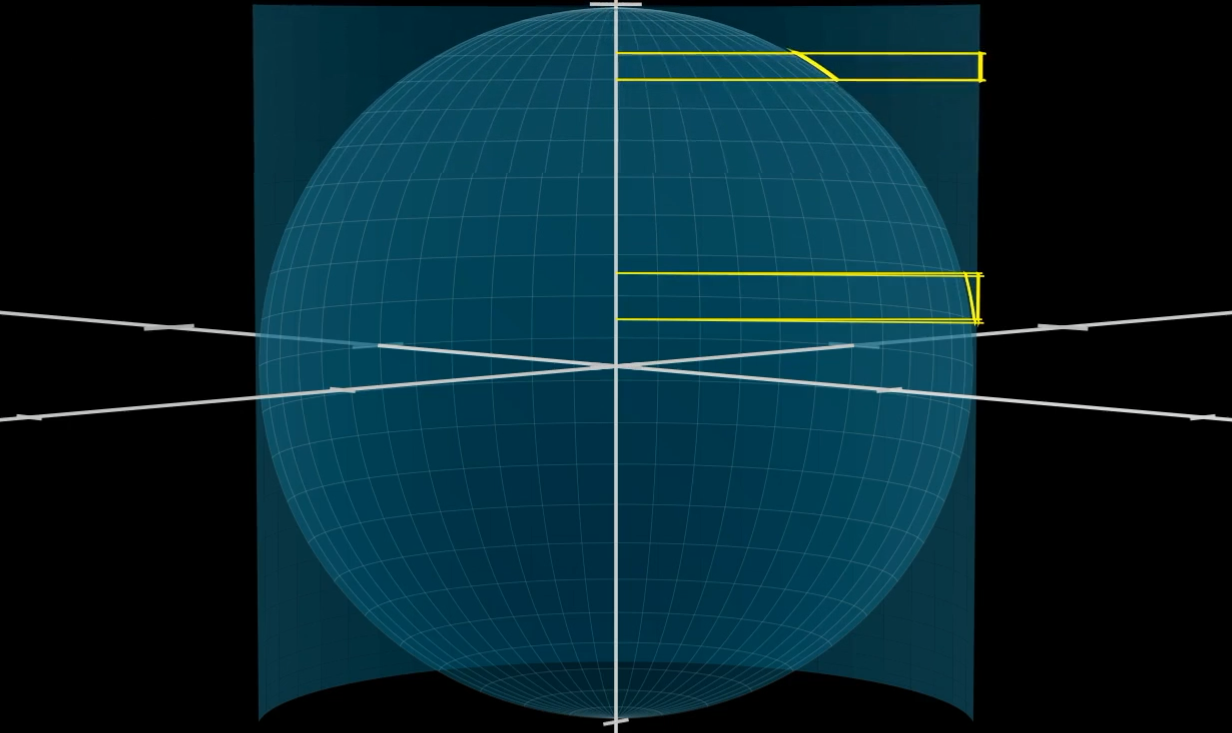
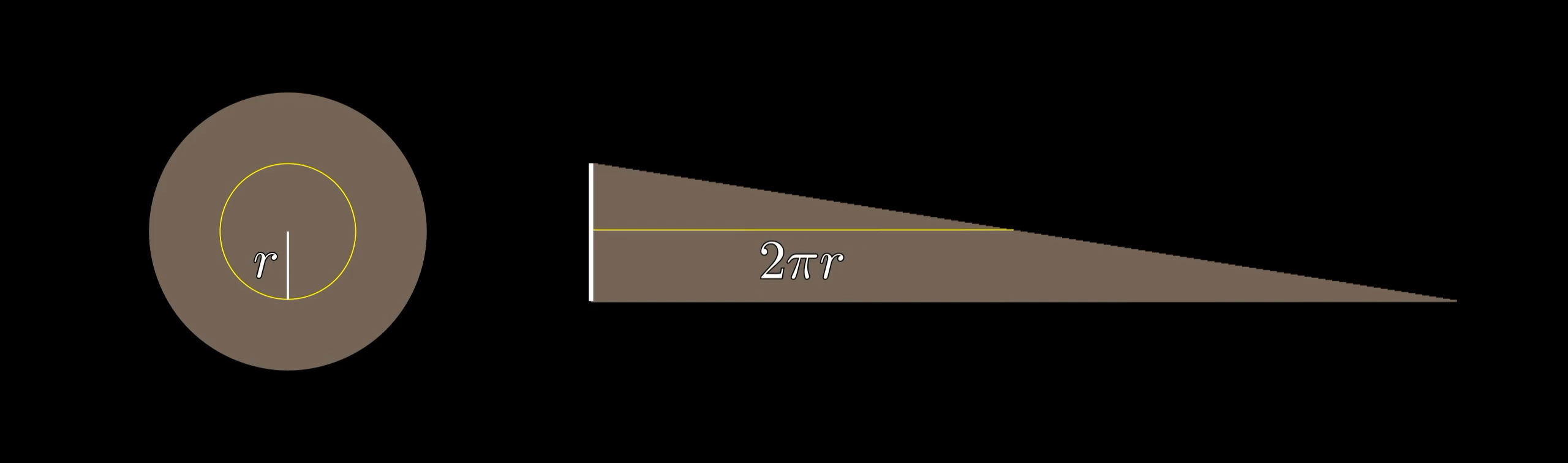
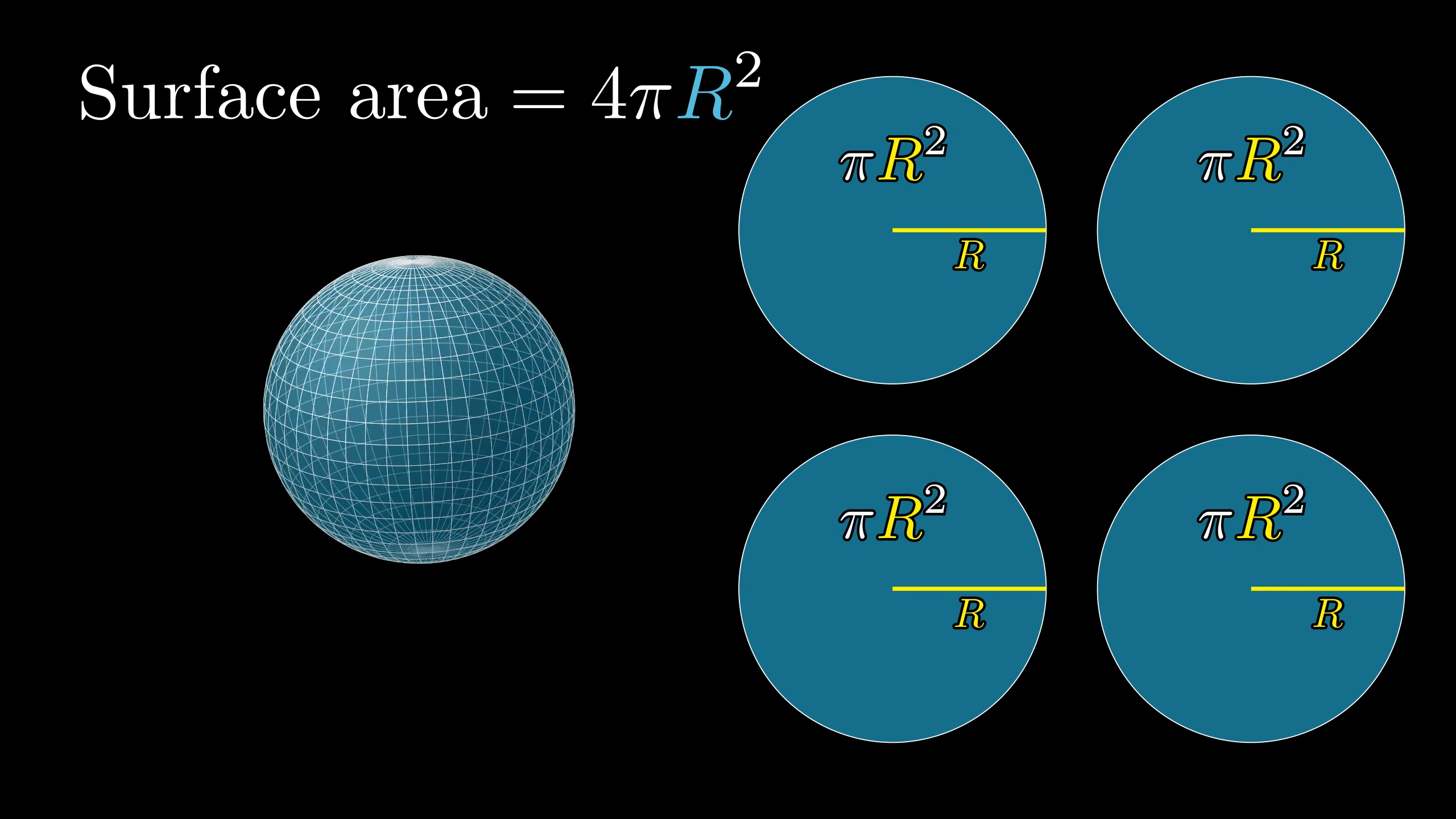
圆柱侧面积(即球的表面积)= \( 4\pi R^2 \),恰好是 4 个半径为 \( R \) 的圆的面积之和:
直观关联:将每个圆“展开”为三角形,4 个这样的三角形可完美拼接成圆柱展开后的矩形